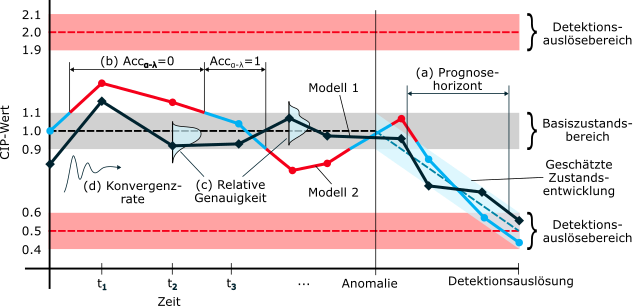
Obwohl Überwachungsdaten wertvolle Informationen über das strukturelle Verhalten liefern, können Simulationsmodelle die Messdaten ergänzen und erweitern, um umfassendere Einblicke zu ermöglichen. Kontinuierlich aktualisierte Simulationsmodelle im Kontext digitaler Zwillinge erlauben die Installation virtueller Sensoren im Simulationsmodell, wodurch die Vorhersage von Größen ermöglicht wird, die schwer messbar sind. Das sind z. B. Spannungen an Positionen, die mit der aktuellen Sensoranordnung nicht zugänglich sind, oder die Prognose der Entwicklung von Zustandsindikatoren (CIPs) als Planungsgrundlage und zur Wartungsplanung. Die Etablierung eines digitalen Zwillings innerhalb des SPP erfordert die Integration mehrerer Simulationsmodelle aus verschiedenen Teilprojekten, die jeweils unterschiedliche Aspekte fokussieren. Die Genauigkeit dieser Modelle ist entscheidend für die Gesamtzuverlässigkeit des digitalen Zwillings. Während die für die Planung verwendeten Modelle häufig als Ausgangspunkt dienen können, sind diese Informationen für bestehende Bauwerke oft nicht verfügbar. Selbst wenn vollständige Informationen vorliegen, ist in den meisten Fällen ein iterativer Prozess zur Verbesserung des Modells auf Basis von Messdaten erforderlich. Diese Verbesserung umfasst nicht nur die Aktualisierung von Modellparametern, sondern auch die Überprüfung der Modellannahmen, z. B. des Detaillierungsgrads der Geometrie, der konstitutiven Modelle oder der Rand- und Anfangsbedingungen. Da es stets eine Diskrepanz zwischen experimentellen Daten und den entsprechenden Modellvorhersagen des digitalen Zwillings aufgrund aleatorischer und epistemischer Unsicherheiten geben wird, muss ein zuverlässiges Simulationsmodell diese Unsicherheiten in die CIP-Prognose integrieren. Es werden zudem Metriken entwickelt, um die Modellqualität zu quantifizieren, die Robustheit der Vorhersagen zu schätzen und bei der Erkennung von Anomalien einen Alarm auszulösen. Eine weitere zentrale Herausforderung für die praktische Anwendung der entwickelten mechanischen Modelle besteht in der Berücksichtigung einer thermischen Kompensation, um den Übergang von konstanten Temperaturbedingungen im Labor zu schwankenden Umweltbedingungen zu ermöglichen.

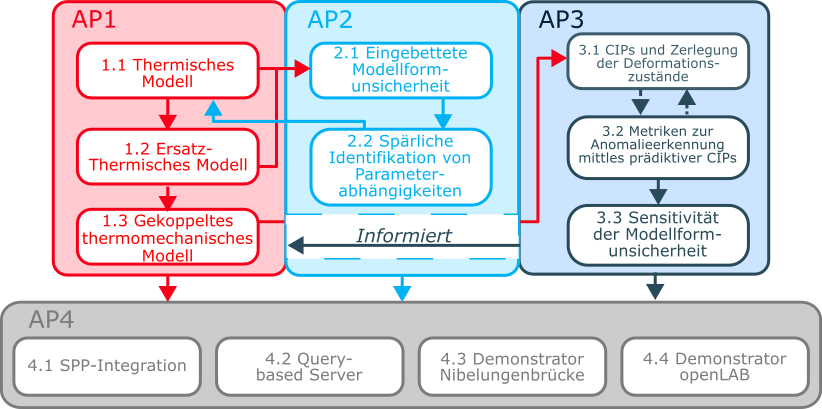
Das Projekt zielt darauf ab, eine Methodik zur iterativen Verbesserung der innerhalb des SPP entwickelten Simulationsmodelle auf Basis kontinuierlicher Überwachungsdaten zu entwickeln, mit einem Fokus auf der Quantifizierung der Unsicherheit der Vorhersagen und Zustandsindikatoren aufgrund von Messfehlern und Modellformunsicherheiten. Zu diesem Zweck beabsichtigen wir, zunächst parametrisierte thermische und thermomechanische Brückenmodelle in Form von Finite-Elemente-Simulationsmodellen zu konstruieren (AP 1). Da deren Auswertung rechenintensiv ist, werden wir auch effiziente Ersatzmodelle untersuchen. Zweitens entwickeln wir Methoden zur Modellaktualisierung und Unsicherheitsquantifizierung unter Modellformunsicherheit auf Basis eingebetteter Bias-Formulierungen (AP 2), wobei wir diese auf höhere Dimensionen und mit Korrelationen in der Einbettung erweitern. Zur Verbesserung der Modelle streben wir eine explizite Identifikation von Parameterabhängigkeiten in Raum, Zeit und Umweltbedingungen an. Drittens definieren wir CIPs basierend auf einer Zerlegung des Deformationszustands, entwickeln Metriken zur Modellqualität und Anomalieerkennung und schätzen die Auswirkungen dieser Unsicherheiten in den eingebetteten Parametern auf die berechneten CIPs (AP 3). Schließlich werden diese Methoden in ein Open-Source-Softwarepaket integriert und zur Verbesserung von Modellen anderer Projekte im SPP einschließlich der Quantifizierung der Unsicherheit angewendet. Zusätzlich werden diese Methoden in die SPP-Demonstratoren (Nibelungenbrücke und openLAB) integriert. Ein abfragebasierter Server wird simulierte vollflächige Temperaturdaten und thermisch kompensierte Deformationen für Partnerprojekte innerhalb des SPP bereitstellen (AP 4).