Data driven model adaptation for identifying stochastic digital twins of bridges

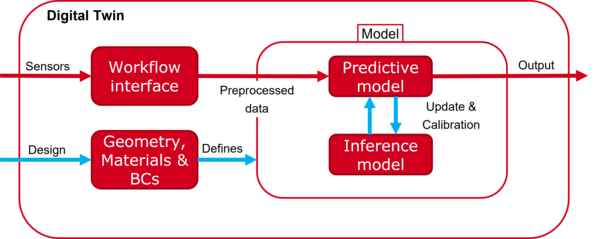
Simulation based techniques are the standard for the design of bridges, primarily related to the mechanical response under different loading conditions. Based on these simulation models, a digital twin of the bridge can be established that has a large potential to increase the information content obtained from regular inspections and/or monitoring data. Potential applications are manifold and include virtual sensor readings at positions that are otherwise inaccessible or are too expensive to equip with a sensor system, investigations of the current performance of the structure, e.g. using the actual loading history in a fatigue analysis instead of the design loads, or planning and prioritizing maintenance measures both for a single bridge as well as for a complete sets of similar bridges. However, once the structure is built, the actual state and/or performance of the structure is usually very different from the design due to various reasons. As a consequence, a digital twin based on the initial simulation model developed in the design usually provides only a limited prediction quality on the future state. It is of utmost importance to incrementally improve the design model until the simulation response of the digital twin matches the sensor readings within certain predefined bounds. This poses many challenges that are addressed in the project.

The first one is the intrinsic uncertainty that is related to both the modelling assumptions (e.g. a linear elastic model) within the digital twin as well as the parameters that are used in these models (e.g.  Young's modulus). An automated procedure based on Bayesian inference will be established that allows to include uncertain sensor data (both from visual inspections as well as from monitoring systems) into a stochastic updating of model parameters that subsequently enables the computation of probability distributions instead of deterministic values. In particular, it is important to derive a methodology that can handle a constant stream of monitoring data, i.e. a continuous updating procedure. As a consequence, key performance indicators derived from the digital twin as a basis for decision making are equipped with an uncertainty. Based on accurate and optimally placed sensors as well as realistic modelling assumptions, this uncertainty can often be reduced.

As there is no ''correct'' model, finding a good one is a complex process that involves several iterations between model improvement and testing. Visually comparing simulation results from calibrated models with experimental data is challenging. In particular, the identification of model deficiency is limited to a reasonable number of data sets that can be visually analyzed. It is important to identify, a) where the simulation model is wrong and b) what are potential improvements to the model. The identification of sources of a model deficiency in a) is complicated by the large amount of data usually available in monitoring systems, and the fact that modelling assumptions (e.g. related to the boundary conditions such as fixed vs flexible support) often trigger sensor discrepancies at locations that are not coinciding with the location of the model error. The identification of potential improvements in b) is based on machine learning techniques. The idea is to support the engineer developing physics-based models to understand what are relevant physical phenomena that are not correctly represented in the model. This includes spatially variable model parameters via random fields or dictionary approaches for constitutive laws, where the most likely model improvement is selected from a dictionary of parameterized functions.

In order to perform the stochastic analysis for complex structures, and in particular for quasi-realtime applications, computational efficiency is of utmost importance, i.e. the computation time of a single evaluation of the digital twin should be as fast as possible. As a consequence, response surfaces are developed that are trained on the computationally expensive forward model and can then be used in a subsequent evaluation to replace the forward model. This requires goal-oriented error estimates for bounding the approximation error incurred by the response surface. A solution for this task is the development of metamodels based on Gaussian Processes or Physics Informed Neural Networks.

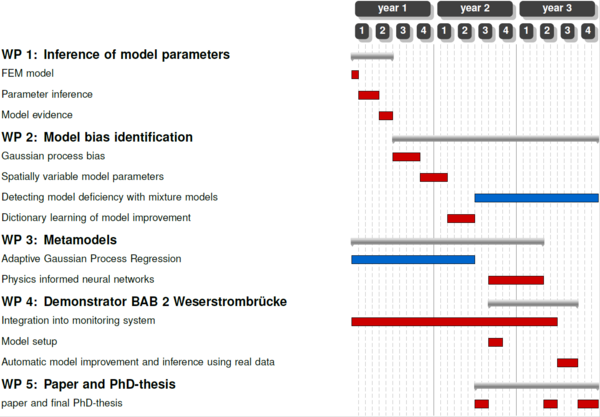
For this project, four work packages are planned as Figure 2 shows.

(Kopie 1)

Project Milestones within the SPP Framework:

• Improved the reliability and quantified the quality of simulation based digital twins for bridges by introducing model form uncertainty into the process of identifying the model parameters from monitoring data. This allows the models to reflect the actual variability seen in field measurements and enables a prediction of KPIs with realistic error bounds as a basis for decision making.
• Developed an adaptive Gaussian process approach that creates fast, reliable approximations of complex bridge models for use in monitoring and assessment. These surrogate models are a precondition for building simulation based digital twins requiring quasi real-time computations with tight precision constraints.
• Used Gaussian Mixture Models and the quantified model form uncertainties to guide potential model improvements for the digital twin. This approach helped identify where the simulation deviated most from real bridge behavior, allowing targeted refinement of the digital twin to better support condition assessment.
• Demonstrated the full calibration process, including model form uncertainty, on a simplified thermal model of the Nibelungenbrücke using real monitoring data. This led to accurate, uncertainty-aware predictions of the thermal behavior, showing how calibrated models can enhance the interpretation of sensor data and support better assessment of current and future bridge's state.